摘錄自:Geometry Concepts: Basic Concepts、Computer Graphics: 向量運算
向量
可以用座標型式 (x, y) 表示,向量相加也可以直接用座標相加:(x1+x2, y1+y2)。
向量內積(dot product)
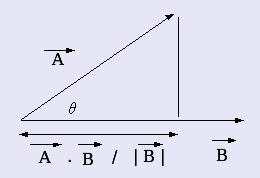
向量 A=(x1, y1)、向量 B=(x2, y2),則 A 與 B 的內積為:A‧B = x1*x2 +y1*y2 = |A||B|Cos(θ),是一個值。又因為 Cos(90) = 0、Cos(0) = 1,所以垂直的兩個向量內積為 0、平行的兩個向量內積有最大值。並且內積公式不限於二維向量,在多維中也可套用。
在電腦圖學中,向量內積可以用來算投影或者光線照射量。光源照射方向若與平面法向量(垂直平面的向量)內積為 0,表示光源與平面平行,照不到平面,絕對值越大,平面受光量越大。

向量外積(cross product)
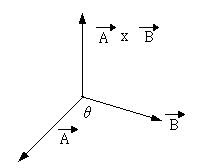
外積公式:A x B = x1*y2 - y1*x2 = |A||B|Sin(θ)。得到的結果是一個向量,向量大小(magnitude)是計算結果,方向則為 z 軸方向(但在 2D 平面中被忽略)。三維空間的外積計算為:A x B = (y1z2-z1y2, z1x2-x1z2, x1y2-y1x2)
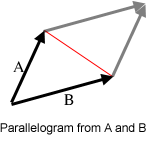
|θ|表示的雖然是向量 A、B 之間的角度,但 θ 本身的正負值則根據右手定則決定。而 |A||B|Sin(θ) 正好就是向量 A、B 圍出來的平行四邊形面積。
圖學中利用向量外積來判定凸面體的某個平面是否為可視平面。利用外積求得平面的法向量,若視線是從 z 軸正向往負向看,該法向量的 z 軸分量為正表示平面正對的視線(看的到),為負表示背對(看不到)。
線與點的距離
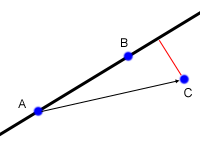
計算一個點到一條直線的距離可以用外積算出,其實就是算 |AC|*Sin(θ) = (AB x AC)/|AB|。
但是要算「線段 AB」到點 C 的距離會有些特殊情況要考慮。例如像下面這個點不是落在 AB 線段中,那最近的距離應該是點 C 到 B 的距離。要判斷這種情況則可以用內積來算。若 AB‧BC 大於 0,表示 AB 與 BC 的夾角 θ介於 90 度到 -90 度之間(注意是 AB 向量,不是 BA 向量,所以是三角形 ABC 的外角),因此可判斷 C 點落在線段 AB 之外且靠近 B。同理類推,計算 BA‧AC 的值,可判斷 C 點是否比較靠近 A 且落在線段外。
多邊形面積
可以利用外積公式來求多邊行面積,即使是凹多邊形也一樣可以。把點依照一個順時針或逆時針方向依序排好,以第一個點為頂點將多邊形切成數個三角形,一一對這些三角形以 A 為向量頂點做外積求出面積。求出來的值無論正負都無妨,全部累計起來後再取絕對值自然會抵消。如下圖:ABC、ACD為負、ADE為正,累加之後取絕對值就是三角形ABC + ACD - ADE = ABCDE 的面積。
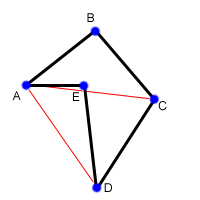
註:在取絕對值之前,若該值為負表示多邊形的頂點是依照順時針方向排序。
向量
可以用座標型式 (x, y) 表示,向量相加也可以直接用座標相加:(x1+x2, y1+y2)。
向量內積(dot product)
向量 A=(x1, y1)、向量 B=(x2, y2),則 A 與 B 的內積為:A‧B = x1*x2 +y1*y2 = |A||B|Cos(θ),是一個值。又因為 Cos(90) = 0、Cos(0) = 1,所以垂直的兩個向量內積為 0、平行的兩個向量內積有最大值。並且內積公式不限於二維向量,在多維中也可套用。
在電腦圖學中,向量內積可以用來算投影或者光線照射量。光源照射方向若與平面法向量(垂直平面的向量)內積為 0,表示光源與平面平行,照不到平面,絕對值越大,平面受光量越大。


向量外積(cross product)
外積公式:A x B = x1*y2 - y1*x2 = |A||B|Sin(θ)。得到的結果是一個向量,向量大小(magnitude)是計算結果,方向則為 z 軸方向(但在 2D 平面中被忽略)。三維空間的外積計算為:A x B = (y1z2-z1y2, z1x2-x1z2, x1y2-y1x2)
|θ|表示的雖然是向量 A、B 之間的角度,但 θ 本身的正負值則根據右手定則決定。而 |A||B|Sin(θ) 正好就是向量 A、B 圍出來的平行四邊形面積。
圖學中利用向量外積來判定凸面體的某個平面是否為可視平面。利用外積求得平面的法向量,若視線是從 z 軸正向往負向看,該法向量的 z 軸分量為正表示平面正對的視線(看的到),為負表示背對(看不到)。


線與點的距離
計算一個點到一條直線的距離可以用外積算出,其實就是算 |AC|*Sin(θ) = (AB x AC)/|AB|。
但是要算「線段 AB」到點 C 的距離會有些特殊情況要考慮。例如像下面這個點不是落在 AB 線段中,那最近的距離應該是點 C 到 B 的距離。要判斷這種情況則可以用內積來算。若 AB‧BC 大於 0,表示 AB 與 BC 的夾角 θ介於 90 度到 -90 度之間(注意是 AB 向量,不是 BA 向量,所以是三角形 ABC 的外角),因此可判斷 C 點落在線段 AB 之外且靠近 B。同理類推,計算 BA‧AC 的值,可判斷 C 點是否比較靠近 A 且落在線段外。

多邊形面積
可以利用外積公式來求多邊行面積,即使是凹多邊形也一樣可以。把點依照一個順時針或逆時針方向依序排好,以第一個點為頂點將多邊形切成數個三角形,一一對這些三角形以 A 為向量頂點做外積求出面積。求出來的值無論正負都無妨,全部累計起來後再取絕對值自然會抵消。如下圖:ABC、ACD為負、ADE為正,累加之後取絕對值就是三角形ABC + ACD - ADE = ABCDE 的面積。

註:在取絕對值之前,若該值為負表示多邊形的頂點是依照順時針方向排序。
