TopCoder Algorithm Tutorials - 基本幾何學(1)

摘錄自：Geometry Concepts: Basic Concepts、Computer Graphics: 向量運算

向量
可以用座標型式 (x, y) 表示，向量相加也可以直接用座標相加：(x₁+x₂, y₁+y₂)。

向量內積(dot product)
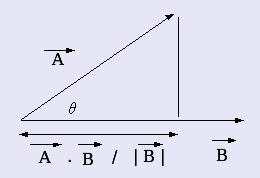
向量 A=(x₁, y₁)、向量 B=(x₂, y₂)，則 A 與 B 的內積為：A‧B = x₁*x₂ +y₁*y₂ = |A||B|Cos(θ)，是一個值。又因為 Cos(90) = 0、Cos(0) = 1，所以垂直的兩個向量內積為 0、平行的兩個向量內積有最大值。並且內積公式不限於二維向量，在多維中也可套用。

在電腦圖學中，向量內積可以用來算投影或者光線照射量。光源照射方向若與平面法向量(垂直平面的向量)內積為 0，表示光源與平面平行，照不到平面，絕對值越大，平面受光量越大。

　

(... 閱讀「TopCoder Algorithm Tutorials - 基本幾何學(1)」全文)

TopCoder Algorithm Tutorials - 基礎數學

摘錄自：Mathematics for TopCoders

底數(base)
把 b 進位的數字轉成十進位，可以用下面這段 code 實現。簡單來說就是利用 mod 10 取出各個位數的數字，乘上 b 的 x 次方(multiplier)得到真正的值加到結果(result)中。

public int toDecimal(int n, int b)
{
   int result = 0;
   int multiplier = 1;
      
   while(n>0)
   {
      result += n % 10 * multiplier;
      multiplier *= b;
      n /= 10;
   }
      
   return result;
}

(... 閱讀「TopCoder Algorithm Tutorials - 基礎數學」全文)

[JavaScript] Callback Notes (with jQuery)

參考：Tutorials:How jQuery Works

Callback Function
callback function 當作參數傳給 parent function 時，像這樣：

$.get('myhtmlpage.html', myCallBack);

但是如果這個 callback function 本身也需要傳參數，則不能寫成

$.get('myhtmlpage.html', myCallBack(param1, param2));  // wrong!!

因為這樣是表示先呼叫 myCallBack，執行後的回傳結果當做 get 的第二個參數。正確的寫法應該是：

$.get('myhtmlpage.html', function(){
  myCallBack(param1, param2);
});

(... 閱讀「[JavaScript] Callback Notes (with jQuery)」全文)

TopCoder Algorithm Tutorials - 解題規劃

摘錄自：Planning an Approach to a TopCoder Problem

Pattern Mining and the Wrong Mindset
當解過一定數量的問題後，會發現問題大致上可以分成幾類，於是就會陷入一種「從過去類似問題中找解法」的情況，試著拿過去解過的問題套到眼前的這個問題。這樣的情況並不是很好，特別是當眼前的問題是一個全新的問題時，很容易產生挫敗感。唯有不斷的複習、把每個問題都當成全新的經驗，才能持續進步。

Coding Kata
試試看下面這個練習，它能帶你體驗面對問題的各種可能情況。
嘗試挑一個未解過的問題，開始思考、尋找解法，把解法寫出來、通過測試之後，記下總共花了多少時間解這個問題。接著把程式碼清掉、再寫一次！第二次可能還是會犯些小錯誤，最後再次通過測試後，同樣記下第二次所花的時間，接著再把程式碼清除重新寫一次。第三次就會覺得順多了，完成後也同樣記錄時間。第一個時間表示當你心中沒有任何解法時，理解問題並思考、設計一個解所需要的時間；第二個時間，很意外地，通常只是少了理解問題的時間；而第三次才是真正的當你面對一個問題且能馬上想到解法時，所需要花的時間以及帶給你的感受，記住這個感受作為日後解題時的鼓勵！

(念到Atomic Code開始)

(... 閱讀「TopCoder Algorithm Tutorials - 解題規劃」全文)

TopCoder Algorithm Tutorials - 從題目線索中找解法

摘錄自：How To Find a Solution

從題目給的線索中猜測該用什麼演算法解題。

直覺模擬
這類題目單純地會給很多步驟，條件(複雜度)不會太高，也不會太低，通常是在測試你的 coding 速度，因此不用想太多，照著做就對了。

BFS (廣度優先搜尋)
這類題目通常要求找出從起點狀態到終點狀態「最少步驟(最低成本)」的解，並且狀態間的轉移成本通常是1。常見題目都是給一個 N*M 的表格，有些格子不能通過，求要到達目的地的最短路徑。
因為 BFS 複雜度多半是線性的，因次 N (或 M) 很大(到百萬)也沒關係。

Flood Fill
BFS 找所有解，而非最小那個。

暴力搜尋、backtracking
暴力搜尋的條件(複雜度)不能太高，因為它就是(必須/可以)嘗試所有可能、然後找最好的。backtracking 也是暴力搜尋的一種，通常用遞迴做，並且題目給的條件(複雜度)會很低，那就很適合。

(... 閱讀「TopCoder Algorithm Tutorials - 從題目線索中找解法」全文)

TopCoder Algorithm Tutorials - 序

摘錄自：The Importance of Algorithms

執行時間分析
當 N = 100 時，各種複雜度的估計執行時間：


最短路徑
即使是目前最好的演算法也不一定能有效解決真實生活中的問題。通常處理這些真實問題時，會加一些 heuristic 來幫助加快找到可行的答案。

字串比對
使用 DP 可以大大節省時間。DNA 比對、文章嫖竊判定...等都是字串比對的應用，「版本比對」則是把"一行"視為一個"字"，因此也是用字串比對的方式去看哪幾行有新增、修改、刪除。

(... 閱讀「TopCoder Algorithm Tutorials - 序」全文)

Selenium Docs (4) - Selenium Grid

原文：Selenium Grid - How It Works

Selenium-RC 的問題

• RC 控制 browser 很慢，除非你的網路或者網站本來就慢，否則 RC 會變成測試上的瓶頸(bottleneck)。
• 一個 RC 上面能「同時執行」的測試有限，實際上開啟超過 6 個瀏覽器就會影響效能。(在 IE 上更慘)
• 如果要開很多個 RC 來避開上述問題當然也是可以，不過維護這麼多個 RC 會很困難。

Selenium Grid 繼承 RC 的好處

• 測試程式、測試網站、RC/瀏覽器是透過 http 聯繫的，所以可以在不同機器上面。
• 測試程式跟網站是跟某個專案有關，但是 RC 跟瀏覽器與專案無關，所以架設起來之後可以很多個專案共用。

(... 閱讀「Selenium Docs (4) - Selenium Grid」全文)

Selenium Docs (3) - 測試設計考量與自訂功能

靜態頁面與動態頁面
存取靜態頁面上面的元件時，可以直接利用 id 定址，而動態頁面則因為每次載入的內容不同，element id 可能會跟著變動，因此必須依靠程式拿到頁面內容過濾後，找出要存取的元件。

AJAX 頁面測試
對於含有 AJAX 的頁面進行測試時，因為其資料是非同步更新，也不會造成頁面 reload，因此在存取元件時要特別小心。設定一個等待時間中止整個測試 thread 並不是一個好方法，因為無法時間是預期的。應該要時時去偵測想要存取的元素是否已經出現，會比較好。

UI Mapping
對於一些常用的網頁元件，例如登入欄位/按鈕，可以用 property 檔案來描述它們，避免直接在程式碼中定位(locator)它們，好處是：

1. 避免這些常用元件散落在程式中。
2. 承上，集中管理易於維護。
3. 元件可以重新命名為較容易看懂的名稱，增加程式可讀性。

直接看原本的例子會更清楚。

Data Driven Testing
自動測試可以輔助手動測試，但當輸入資料有多筆時，要把資料跟程式內容分開，另外寫到一個檔案中。

資料庫驗證
可以直接利用程式存取資料庫的內容，作為測試的資料來源。例如做登入頁面測試時，可以拿資料庫已經註冊的帳號登入看看是否可以登入，或者拿未註冊成功的資料登入看看是否無法登入。

自訂功能
Selenium 允許自訂一些動作或定址方式，只要在他們的 object prototype 裡面加入自訂的 JavaScript 函數，並把函數依照規定命名。可以自訂的有：action、Accessors/Assertions、locator。

(... 閱讀「Selenium Docs (3) - 測試設計考量與自訂功能」全文)

[轉錄] 軟體測試基於 Web 的系統測試方法

原文依據：Web Testing: Complete guide on testing web applications
本文原文：软件测试基于Web的系统测试方法

基於 Web 的系統測試與傳統的軟體測試既有相同之處，也有不同的地方，對軟體測試提出了新的挑戰。基於 Web 的系統測試不但需要檢查和驗證是否按照設計的要求運行，而且還要評價系統在不同用戶的流覽器端的顯示是否合適。重要的是，還要從最終用戶的角度進行安全性和可用性測試。

本文從功能、性能、可用性、用戶端相容性、安全性等方面討論了基於 Web 的系統測試方法。

(... 閱讀「[轉錄] 軟體測試基於 Web 的系統測試方法」全文)

Selenium Docs (2) - Remote Control (RC)

Selenium RC 組成

• Selenium Server：負責打開/關閉瀏覽器、接受並執行指令，就像一個 HTTP proxy。在打開瀏覽器時會在這個瀏覽器中綁上 Selenium-Core， 這個 Selenium-Core 其實就是一堆 JavaScript 函式，幫你把 client 端傳來的指令換成瀏覽器可以執行的 JavaScript 指令。(目前 Selenium Server 是 .jar 檔案，因此要執行它必須有 JVM。)
• Client libraries：提供一些 API 讓你可以用自己的程式語言與 Server 溝通。目前提供 Java、Python、C#、Ruby、PHP、Perl 等六個語言的 API。

回報結果
Selenium 沒有特別提供這種機制，但可與其它 Test Framework Reporting 工具結合。例如 Java 有 JUnit、TestNG...等。(參考支援的 Testing Frameworks)
題外話：Selenium IDE 有個很不錯的測試環境：Bromine，特別被 Selenium 支援。可以設定 test case 要做什麼事情、在哪些平台上執行、甚至分開到多個 server 同時執行，並且實際執行後回報結果。

在測試程式中執行 JavaScript
用 getEval(JavaScriptCode) 可以執行一段 JavaScript 程式，並得到它的回傳結果。例如可以用在取得動態網頁元素的 id、或者網頁上的圖片數目(有例子)。另外 JavaScript code 中記得用 window 物件來取得 dom，以免拿到不是測試視窗的內容。

(... 閱讀「Selenium Docs (2) - Remote Control (RC)」全文)

[JavaScript] Chapter 6&7 Notes

Reference: JavaScript - The Definitive Guide Chapter 6, Chapter 7

for/in loop: (section 6.9)

1. 可以動態改變指定的 variable，例如下面這段程式碼複製 obj 的所有屬性名稱到 arr 中。
   

     var obj = {x:1, y:2, z:3};
     var arr = new Array( );
     var i = 0;
     for(arr[i++] in obj) /* empty loop body */;
   

2. for/in 存取 property 並沒有依照某個順序，完全是 implementation-dependent，所以在 loop 中新增/刪除某個 property 要好好考慮。

with 指令會暫時改變 scope chain，雖然程式碼比較好寫，但執行效率會變差，盡量不要用。(section 6.18)

當 object 用 obj["prop"] 來存取時，"prop"可以做 string 的操作，例如 obj["prop"+i] 動態決定要存取什麼屬性。如果用 obj.prop 的寫法，則 prop 當然是寫死的文字。這就是兩種 object 存取方式的差別。(section 7.3)

所有自訂的 object 屬性都是 enumerable 的 (ie. 可使用 for/in loop 存取)；Nonenumerable 屬性指的是繼承 Object class 來的那些屬性。所以 propertyIsEnumerable()(某自訂屬性是否 enumerable) 得到的結果幾乎會跟 hasOwnProperty() (是否有某個自訂屬性)一樣。(section 7.4)

(... 閱讀「[JavaScript] Chapter 6&7 Notes」全文)

[JavaScript] try/catch/finally

Reference: JavaScript - The Definitive Guide, Section 6.17

try/catch/finally 的執行示意圖：(四種情況)

(... 閱讀「[JavaScript] try/catch/finally」全文)

[JavaScript] Variable Scope

Reference: JavaScript - The Definitive Guide, Section 4.3

function 內宣告的 var scope 是整個 function 的，舉例如下：

var scope = "global";
function f( ) {
  alert(scope);   // Displays "undefined", not "global"
  var scope = "local";  // Variable initialized here, but defined everywhere
  alert(scope);  // Displays "local"
}
f( );

第一個 alert(scope); 會 undefine 是因為下面那一行宣告的關係，
就是說，這時候下面那行的 scope 已經宣告了，只是還沒初始。

(... 閱讀「[JavaScript] Variable Scope」全文)

Selenium Docs (1) - 基本介紹

Selenium 介紹
Selenium 包含三大部分：(1) Selenium-IDE；(2) Selenium-RC；(3) Selenium-Grid。

• Selenium-IDE：Firefox 的附加元件，可以錄下操作網頁的動作作為 test cases，也可以自己編輯這些 test cases。
• Selenium-RC：讓會寫程式的人利用現有的程式語言做自動化測試，selenium 提供 API 並支援多種語言 (HTML, Java、C#、Perl、PHP、Python、Ruby) 方便寫 test cases。
• Selenium-Grid：平行測試、跨瀏覽器測試。

Selenium 指令 (Selenese)
指令有三種型態：(1) 動作 Actions；(2) 存取 Accessors；(3) 判斷 Assertions。

• 動作：用來操作頁面，例如：點擊(click)、輸入(type) ...等動作。如果動作執行出問題，這個測試會被中止。
• 存取：查看目前頁面的狀態，或者把頁面內容存起來，例如 storeTitle。也會被用來判斷(Assertions)。
  
• 判斷：類似存取(Accessors)，但更進一步地做些檢查，例如看目前頁面的標題是否為X，某個欄位是否被勾選...等。有三種用法：宣稱(assert)、驗證(verify)、等候(waitFor)。宣稱某個正確的內容時，若實際內容與宣稱內容不符合，此測試會中斷。驗證則稍微寬鬆一些，測試會繼續執行而把錯誤存在紀錄的 log 中。等候則用來確認某些內容出現在頁面上(常見的情況是搭配有 ajax 的頁面使用)，當該內容未在設定的時間內出現時 (timeout)，則中斷測試。
  

(... 閱讀「Selenium Docs (1) - 基本介紹」全文)

Selenium Note

[Tutorial] [Documentation] [API] [Forum]

selenium 不能測的功能：
(1) 檔案上傳 - 無法控制 windows file chooser
(2) ActiveX 的操作
(3) applet 的操作
(4) Flash - [對策]
(5) 切換 domain [The Same Origin Policy]

Reference:

Google Developer Talk: http://tw.youtube.com/watch?v=EDb8yOM3Vpw

C. Titus Brown, Gheorghe Gheorghiu, Jason Huggins, An Introduction to Testing Web Applications with twill and Selenium , O'REILLY, 2007. [Google Preview]

(... 閱讀「Selenium Note」全文)